A method by which these kinds of structures can be
constructed is shown in the following U.S. Patent. Link is embedded.
More detailed information on the method will be added to this webpage
as it comes available, as the method is used.
Derivation of formula to calculate the length of the side piece
in the lowest level pentagon
In the embedded video above it is explained that all calculations including the
calculation for the diameter of the dome are obtained from the side length of the
lowest level pentagon starter frustum. On this webpage the derivation is shown for
the length of the starter side piece that will be required, when the diameter of
the dome is chosen. This derivation is titled "Example 10". The reason is that in
the patent specification there are 9 examples with solutions. The video demonstration
leads on from the patent so this derivation is titled "Example 10".

This first diagram shown below provides the basis for this derivation. It is essential to first define the variables for the equations and find "Ls" in relation P1st

In this 1st step an equation for the diameter of the dome is obtained. Then in the 2nd step another equation for the length "Ls" is found now that the width of the 1st level hexagon has been determined
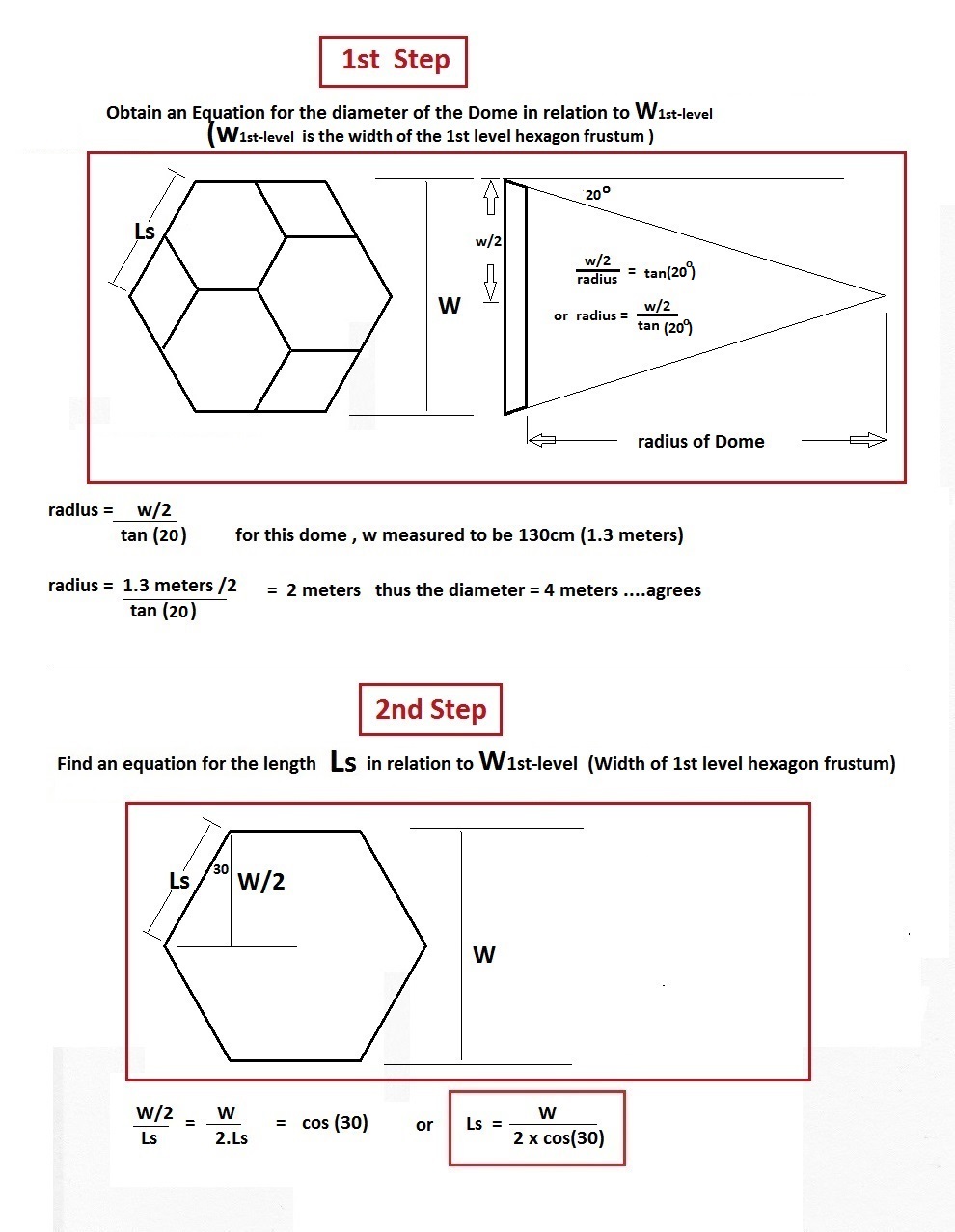
In this 3rd step I have returned to the initial step to find an
an equation for the length of the starter side piece in relation to "Ls".
Then in the 4th step of the derivation I substitute for the unknowns.
In the beginning of the video when the assembly begain, the first pentagon was
placed on top of the crates. This pentagon was constructed from lower level pentagons with
a side length of 300 millimeters. These pentagons have given a dome of 4 meters in
diameter. Using the derived equation you can work back the other way. Suppose that an
Architect wishes to build a dome that is 4 meters in diameter. If we insert 4 meters
into the equation and do the calculation then the calculation should tell us that
the length of the starter side piece that is needed to start with. If the equation
is correct then, this length should be 300 millimeters.
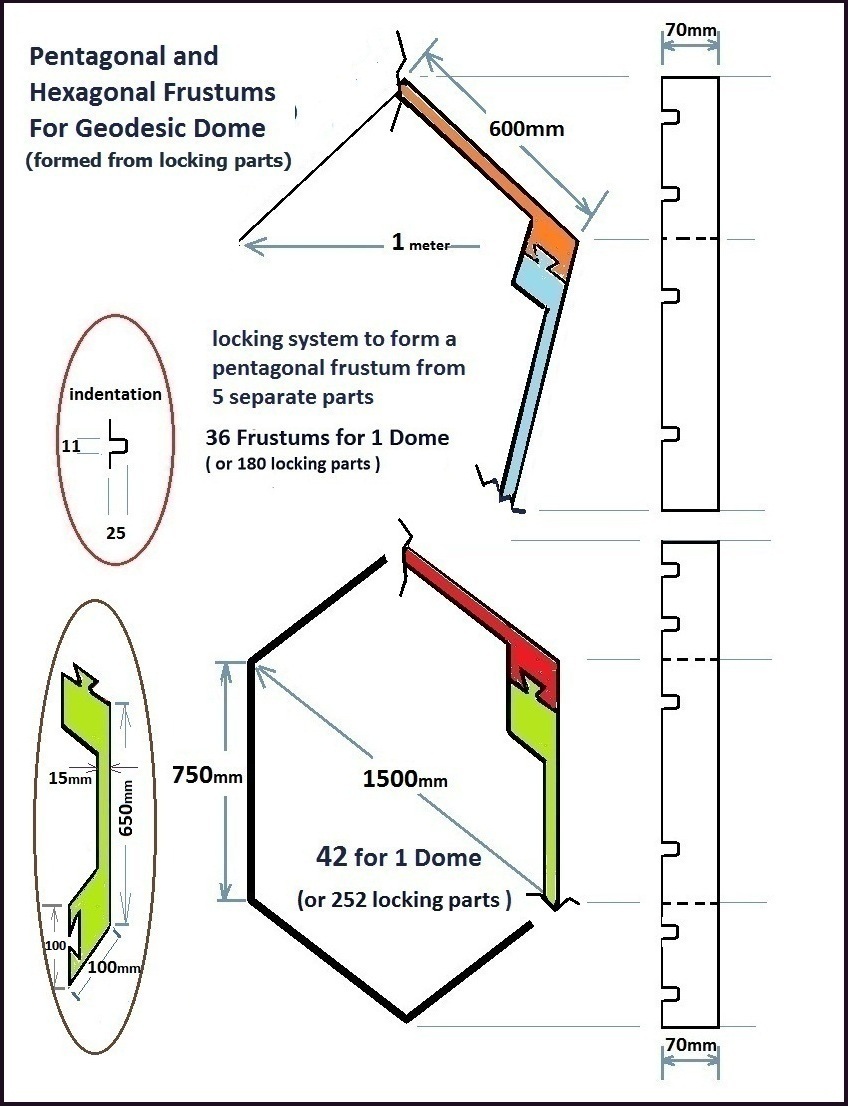
In the case where the Geodesic HoneyComb Skeleton is formed from metal: It is significant to note that the frustums will be tooo big to be manufactured at a conventional foundry. In this case, the frustums will need to be formed from individual parts that I will refer to as locking-Parts There will be 5 locking-parts to form a pentagonal frustum and 6 locking-parts to form a hexagonal frustum. These cast metal Locking-Parts will be hammered into place to form each frustum.....so care must be taken in the design of the casting-patterns so that FIRSTLY ; the locking parts can be hammered together with ease ........and SECONDLY ; the frustum is rigid..... there cannot be movement ......thus this could take a few attempts to get the casting-patterns right
Shown below are suggested designs for the Locking-Parts The dimensions are chosen to obtain a completed dome of 8-meters diameter. Note that the design is such that the joins must be substantial (( as shown in the drawings below )) Otherwise there will be a deformation of the frustums in the lower section of the dome